Dispersion (optics)

In optics, and by analogy other branches of physics dealing with wave propagation, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular.

A medium having this common property may be termed a dispersive medium (plural ''dispersive media'').

Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the pulses of light in optical fiber. Physically, dispersion translates in a loss of kinetic energy through absorption.

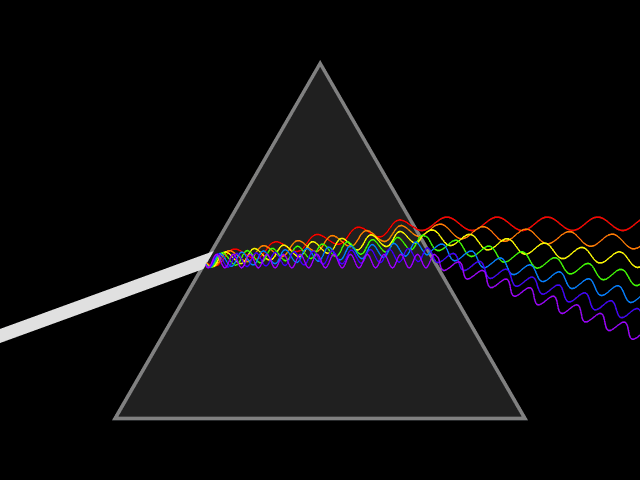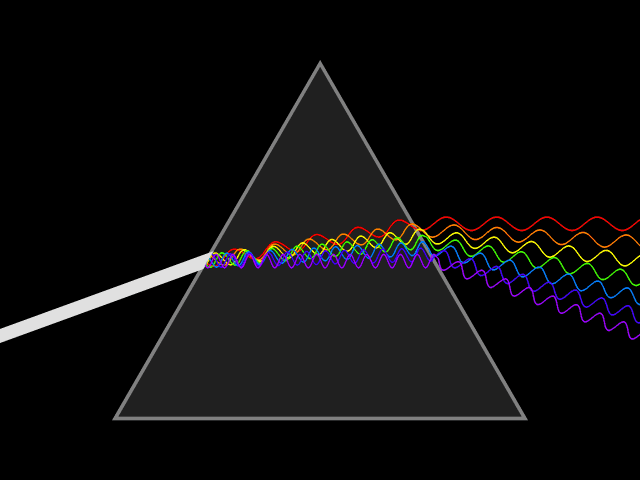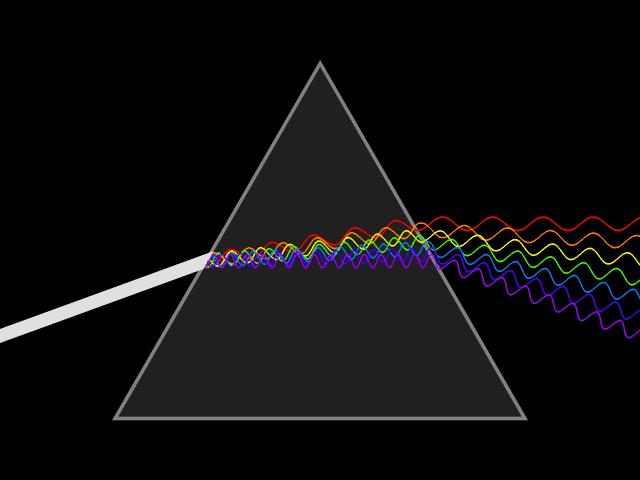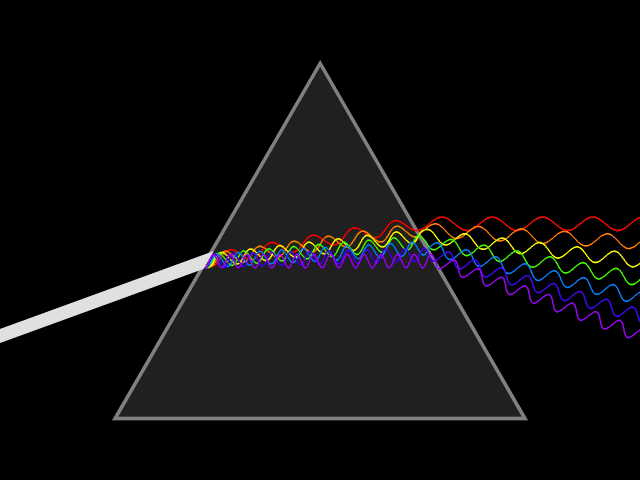
In optics, one important and familiar consequence of dispersion is the change in the angle of refraction of different colors of light, as seen in the spectrum produced by a dispersive prism and in chromatic aberration of lenses. Design of compound achromatic lenses, in which chromatic aberration is largely cancelled, uses a quantification of a glass's dispersion given by its Abbe number ''V'', where ''lower'' Abbe numbers correspond to ''greater'' dispersion over the visible spectrum. In some applications such as telecommunications, the absolute phase of a wave is often not important but only the propagation of wave packets or "pulses"; in that case one is interested only in variations of group velocity with frequency, so-called group-velocity dispersion.

All common transmission media also vary in attenuation (normalized to transmission length) as a function of frequency, leading to attenuation distortion; this is not dispersion, although sometimes reflections at closely spaced impedance boundaries (e.g. crimped segments in a cable) can produce signal distortion with further aggravates inconsistent transit time as observed across signal bandwidth.

Examples

The most familiar example of dispersion is probably a rainbow, in which dispersion causes the spatial separation of a white light into components of different wavelengths (different colors). However, dispersion also has an effect in many other circumstances: for example, group velocity dispersion causes pulses to spread in optical fibers, degrading signals over long distances; also, a cancellation between group-velocity dispersion and nonlinear effects leads to soliton waves.

Material and waveguide dispersion

Most often, chromatic dispersion refers to bulk material dispersion, that is, the change in refractive index with optical frequency. However, in a waveguide there is also the phenomenon of ''waveguide dispersion'', in which case a wave's phase velocity in a structure depends on its frequency simply due to the structure's geometry. More generally, "waveguide" dispersion can occur for waves propagating through any inhomogeneous structure (e.g., a photonic crystal), whether or not the waves are confined to some region. In a waveguide, ''both'' types of dispersion will generally be present, although they are not strictly additive. For example, in fiber optics the material and waveguide dispersion can effectively cancel each other out to produce a zero-dispersion wavelength, important for fast fiber-optic communication.

Material dispersion in optics

Material dispersion can be a desirable or undesirable effect in optical applications. The dispersion of light by glass prisms is used to construct spectrometers and spectroradiometers. However, in lenses, dispersion causes chromatic aberration, an undesired effect that may degrade images in microscopes, telescopes, and photographic objectives.

The ''phase velocity'', ''v'', of a wave in a given uniform medium is given by
:$v = \frac$
where ''c'' is the speed of light in a vacuum and ''n'' is the refractive index of the medium.

In general, the refractive index is some function of the frequency ''f'' of the light, thus ''n'' = ''n''(''f''), or alternatively, with respect to the wave's wavelength ''n'' = ''n''(''λ''). The wavelength dependence of a material's refractive index is usually quantified by its Abbe number or its coefficients in an empirical formula such as the Cauchy or Sellmeier equations.

Because of the Kramers–Kronig relations, the wavelength dependence of the real part of the refractive index is related to the material absorption, described by the imaginary part of the refractive index (also called the extinction coefficient). In particular, for non-magnetic materials ( ''μ'' =  ''μ''₀), the susceptibility ''χ'' that appears in the Kramers–Kronig relations is the electric susceptibility ''χ''_e = ''n''² − 1.

The most commonly seen consequence of dispersion in optics is the separation of white light into a color spectrum by a prism. From Snell's law it can be seen that the angle of refraction of light in a prism depends on the refractive index of the prism material. Since that refractive index varies with wavelength, it follows that the angle that the light is refracted by will also vary with wavelength, causing an angular separation of the colors known as ''angular dispersion''.

For visible light, refraction indices ''n'' of most transparent materials (e.g., air, glasses) decrease with increasing wavelength ''λ'':
:$1 < n(\lambda_) < n(\lambda_) < n(\lambda_)\ ,$

or alternatively:
:$\frac < 0.$

In this case, the medium is said to have ''normal dispersion''. Whereas, if the index increases with increasing wavelength (which is typically the case in the ultraviolet), the medium is said to have ''anomalous dispersion''.

At the interface of such a material with air or vacuum (index of ~1), Snell's law predicts that light incident at an angle ''θ'' to the normal will be refracted at an angle arcsin(). Thus, blue light, with a higher refractive index, will be bent more strongly than red light, resulting in the well-known rainbow pattern.

Group velocity dispersion

Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed group velocity dispersion (GVD). While phase velocity ''v'' is defined as ''v'' = , this describes only one frequency component. When different frequency components are combined, as when considering a signal or a pulse, one is often more interested in the group velocity which describes the speed at which a pulse or information superimposed on a wave (modulation) propagates. In the accompanying animation, it can be seen that the wave itself (orange-brown) travels at a phase velocity which is much faster than the speed of the ''envelope'' (black) which corresponds to the group velocity. This pulse might be a communications signal, for instance, and its information only travels at the group velocity rate even though it consists of wavefronts advancing at a faster rate (the phase velocity).

It is possible to calculate the group velocity from the refractive index curve ''n''(''ω'') or more directly from the wavenumber ''k'' = ''ωn''/''c'' where ''ω'' is the radian frequency ''ω''=2''πf''. Whereas one expression for the phase velocity is ''v_p=ω/k'', the group velocity can be expressed using the derivative: ''v''_g=''dω/dk''. Or in terms of the phase velocity ''v_p'',

:$= \frac .$

When dispersion is present, not only will the group velocity not be equal to the phase velocity, but generally will itself vary with wavelength. This is known as group velocity dispersion and causes a short pulse of light to be broadened, as the different frequency components within the pulse travel at different velocities. Group velocity dispersion is quantified as the derivative of the ''reciprocal'' of the group velocity with respect to radian frequency which results in ''group velocity dispersion'' = .

If a light pulse is propagated through a material with positive group-velocity dispersion, then the shorter wavelength components travel slower than the longer wavelength components. The pulse therefore becomes ''positively chirped'', or ''up-chirped'', increasing in frequency with time. On the other hand, if a pulse travels through a material with negative group-velocity dispersion, shorter wavelength components travel faster than the longer ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.

An everyday example of a negatively chirped signal in the acoustic domain is that of an approaching train hitting deformities on a welded track. The sound caused by the train itself is impulsive, and travels much faster in the metal tracks than in air, so that the train can be heard well before it arrives. However from afar it isn't heard as causing impulses, but leads to a distinctive descending chirp, amidst reverberation caused by the complexity of the vibrational modes of the track. Group velocity dispersion can be heard in that the volume of the sounds stays audible for a surprisingly long time, up to several seconds.

The ''group velocity dispersion parameter'':
:$D = \frac \, \frac.$
is often used to quantify GVD, that is proportional to ''D'' through a negative factor:
:$D = - \frac \, \frac .$

According to some authors a medium is said to have ''normal dispersion''/''anomalous dispersion'' for a certain vacuum wavelength ''λ''₀ if the ''second'' derivative of the refraction index calculated in ''λ''₀ is positive/negative or, equivalently, if ''D''(''λ''₀) is negative/positive. This definition concerns group velocity dispersion and should not be confused with the one given in previous section. The two definitions do not coincide in general, so the reader has to understand the context.

Dispersion control

The result of GVD, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fiber, since if dispersion is too high, a group of pulses representing a bit-stream will spread in time and merge, rendering the bit-stream unintelligible. This limits the length of fiber that a signal can be sent down without regeneration. One possible answer to this problem is to send signals down the optical fibre at a wavelength where the GVD is zero (e.g., around 1.3–1.5 μm in silica fibres), so pulses at this wavelength suffer minimal spreading from dispersion. In practice, however, this approach causes more problems than it solves because zero GVD unacceptably amplifies other nonlinear effects (such as four wave mixing). Another possible option is to use soliton pulses in the regime of negative dispersion, a form of optical pulse which uses a nonlinear optical effect to self-maintain its shape. Solitons have the practical problem, however, that they require a certain power level to be maintained in the pulse for the nonlinear effect to be of the correct strength. Instead, the solution that is currently used in practice is to perform dispersion compensation, typically by matching the fiber with another fiber of opposite-sign dispersion so that the dispersion effects cancel; such compensation is ultimately limited by nonlinear effects such as self-phase modulation, which interact with dispersion to make it very difficult to undo.

Dispersion control is also important in lasers that produce short pulses. The overall dispersion of the optical resonator is a major factor in determining the duration of the pulses emitted by the laser. A pair of prisms can be arranged to produce net negative dispersion, which can be used to balance the usually positive dispersion of the laser medium. Diffraction gratings can also be used to produce dispersive effects; these are often used in high-power laser amplifier systems. Recently, an alternative to prisms and gratings has been developed: chirped mirrors. These dielectric mirrors are coated so that different wavelengths have different penetration lengths, and therefore different group delays. The coating layers can be tailored to achieve a net negative dispersion.

In waveguides

Waveguides are highly dispersive due to their geometry (rather than just to their material composition). Optical fibers are a sort of waveguide for optical frequencies (light) widely used in modern telecommunications systems. The rate at which data can be transported on a single fiber is limited by pulse broadening due to chromatic dispersion among other phenomena.

In general, for a waveguide mode with an angular frequency ''ω''(''β'') at a propagation constant ''β'' (so that the electromagnetic fields in the propagation direction ''z'' oscillate proportional to ''e''^{''i''(''βz''−''ωt'')}), the group-velocity dispersion parameter ''D'' is defined as:
:$D = -\frac \frac = \frac \frac$

where ''λ'' =  is the vacuum wavelength and ''v''_g =  is the group velocity. This formula generalizes the one in the previous section for homogeneous media, and includes both waveguide dispersion and material dispersion. The reason for defining the dispersion in this way is that , ''D'', is the (asymptotic) temporal pulse spreading Δ''t'' per unit bandwidth
Δ''λ'' per unit distance travelled, commonly reported in ps/ nm/ km for optical fibers.

In the case of multi-mode optical fibers, so-called modal dispersion will also lead to pulse broadening. Even in single-mode fibers, pulse broadening can occur as a result of polarization mode dispersion (since there are still two polarization modes). These are ''not'' examples of chromatic dispersion as they are not dependent on the wavelength or bandwidth of the pulses propagated.

Higher-order dispersion over broad bandwidths

When a broad range of frequencies (a broad bandwidth) is present in a single wavepacket, such as in an ultrashort pulse or a chirped pulse or other forms of spread spectrum transmission, it may not be accurate to approximate the dispersion by a constant over the entire bandwidth, and more complex calculations are required to compute effects such as pulse spreading.

In particular, the dispersion parameter ''D'' defined above is obtained from only one derivative of the group velocity. Higher derivatives are known as ''higher-order dispersion''. These terms are simply a Taylor series expansion of the dispersion relation ''β''(''ω'') of the medium or waveguide around some particular frequency. Their effects can be computed via numerical evaluation of Fourier transforms of the waveform, via integration of higher-order slowly varying envelope approximations, by a split-step method (which can use the exact dispersion relation rather than a Taylor series), or by direct simulation of the full Maxwell's equations rather than an approximate envelope equation.

Generalized formulation of the high orders of dispersion – Lah-Laguerre optics

The description of the chromatic dispersion in a perturbative manner through Taylor coefficients is advantageous for optimization problems where the dispersion from several different systems needs to be balanced. For example, in chirp pulse laser amplifiers, the pulses are first stretched in time by a stretcher to avoid optical damage. Then in the amplification process, the pulses accumulate inevitably linear and nonlinear phase passing through materials. And lastly, the pulses are compressed in various types of compressors. To cancel any residual higher orders in the accumulated phase, usually individual orders are measured and balanced. However, for uniform systems, such perturbative description is often not needed (i.e., propagation in waveguides).
The dispersion orders have been generalized in a computationally friendly manner, in the form of Lah-Laguerre type transforms.

The dispersion orders are defined by the Taylor expansion of the phase or the wavevector.

$\begin\varphi \mathrm\omega\mathrm = \varphi\left.\ \_ + \left. \ \frac \_\left(\omega - \omega_ \right) + \frac\left. \ \frac \_ \left(\omega - \omega_ \right)^\ + \ldots + \frac\left. \ \frac \_ \left(\omega - \omega_ \right)^ + \ldots \end$

$\begink\mathrm\omega\mathrm = k\left.\ \_ + \left. \ \frac \_ \left(\omega - \omega_ \right) + \frac\left. \ \frac \_ \left(\omega - \omega_ \right)^\ + \ldots + \frac\left. \ \frac \_ \left(\omega - \omega_ \right)^ + \ldots \end$

The dispersion relations for the wavector $k \mathrm\omega\mathrm = \fracn \mathrm\omega\mathrm$ and the phase
$\varphi \mathrm\omega\mathrm = \frac \mathrm\omega\mathrm$ can be expressed as:

$\begin\frack \mathrm\omega \mathrm=\frac\left(p\fracn \mathrm\omega \mathrm+\omega \fracn \mathrm\omega \mathrm\right)\ \end$,
$\begin\frac\varphi \mathrm\omega \mathrm = \frac\left(p\frac \mathrm\omega \mathrm+\omega \frac \mathrm\omega \mathrm\right) \end (1)$

The derivatives of any differentiable function $f\mathrm\omega \mathrm\lambda \mathrm$ in the wavelength or the frequency space is specified through a Lah transform as:

$\begin \fracf \mathrm\omega \mathrm=^p^p\sum\limits^p_\end$ $,$
$\begin \fracf \mathrm\lambda \mathrm=^p^p\sum\limits^p_\end (2)$

The matrix elements of the transformation are the Lah coefficients: $\mathcal\mathrmp,m\mathrm = \frac\frac$

Written for the GDD the above expression states that a constant with wavelength GGD, will have zero higher orders. The higher orders evaluated from the GDD are:
$\begin \fracGDD \mathrm\omega \mathrm=^p^p\sum\limits^p_ \end$

Substituting equation (2) expressed for the refractive index $n$ or optical path $OP$ into equation (1) results in closed-form expressions for the dispersion orders. In general the $p^$ order dispersion POD is a Laguerre type transform of negative order two:

$POD = \frac=(-1)^p(\frac)^\sum_^\mathcal (\lambda)^m\frac$ $,$
$POD = \frac=(-1)^p(\frac)^\sum_^\mathcal (\lambda)^m\frac$

The matrix elements of the transforms are the unsigned Laguerre coefficients of order minus 2, and are given as: $\mathcal\mathrmp,m\mathrm = \frac\frac$

The first ten dispersion orders, explicitly written for the wavevector, are:

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(n \mathrm\omega \mathrm+\omega \frac\right) = \frac\left(n \mathrm\lambda \mathrm-\lambda \frac\right) = v^_\end$

The group refractive index $n_g$ is defined as: $n_g = cv^_$.

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac\left(\frac\right)\left(^\frac\right) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac +^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac +\mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right)= \frac^ \Bigl(\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac +\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^ \Bigl(\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+ \mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac +\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+ \mathrm^\frac +\\+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+ \mathrm^\frac+\\+\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\boldsymbol = \frack \mathrm\omega \mathrm = \frac\left(\mathrm\frac+\omega \frac\right) = \frac^\Bigl(\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+ ^\frac+\\+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+ ^\frac\Bigr) \end$

Explicitly, written for the phase $\varphi$, the first ten dispersion orders can be expressed as a function of wavelength using the Lah transforms (equation (2)) as:

$\begin \fracf \mathrm\omega \mathrm=^p^p\sum\limits^p_\end$ $,$
$\begin \fracf \mathrm\lambda \mathrm=^p^p\sum\limits^p_\end$

$\begin\frac= \left(\frac\right)\frac = \left(\frac\right)\frac\end$

$\begin\frac = \frac\left(\frac\right) = ^\left(\mathrm\lambda \frac+^\frac\right) \end$

$\begin\frac= ^\left(\mathrm\lambda \frac+\mathrm^\frac+^\frac\right) \end$

$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac+\mathrm^\frac +^\frac\Bigr) \end$

$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac +\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac\mathrm^\frac\Bigr) \end$

$\begin\frac= ^ \Bigl(\mathrm\lambda \frac+\mathrm^\frac+ \mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+^\frac \Bigr) \end$

$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac+ \mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\\ +^\frac\Bigr) \end$
$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac+ \mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\\+\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

$\begin\frac= ^\Bigl(\mathrm\lambda \frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\mathrm^\frac+\\+\mathrm^\frac +\mathrm^\frac+\mathrm^\frac+^\frac\Bigr) \end$

Spatial dispersion

In electromagnetics and optics, the term ''dispersion'' generally refers to aforementioned temporal or frequency dispersion. Spatial dispersion refers to the non-local response of the medium to the space; this can be reworded as the wavevector dependence of the permittivity. For an exemplary anisotropic medium, the spatial relation between electric and electric displacement field can be expressed as a convolution:

:$D_i(t,r)=E_i(t,r)+ \int_^ \int f_(\tau;r,r')E_k(t-\tau,r')dV'd\tau,$

where the kernel $f_$ is dielectric response (susceptibility); its indices make it in general a tensor to account for the anisotropy of the medium. Spatial dispersion is negligible in most macroscopic cases, where the scale of variation of $E_k(t-\tau,r')$ is much larger than atomic dimensions, because the dielectric kernel dies out at macroscopic distances. Nevertheless, it can result in non-negligible macroscopic effects, particularly in conducting media such as metals, electrolytes and plasmas. Spatial dispersion also plays role in optical activity and Doppler broadening, as well as in the theory of metamaterials.

In gemology

In the technical terminology of gemology, ''dispersion'' is the difference in the refractive index of a material at the B and G (686.7  nm and 430.8 nm) or C and F (656.3 nm and 486.1 nm) Fraunhofer wavelengths, and is meant to express the degree to which a prism cut from the gemstone demonstrates "fire". Fire is a colloquial term used by gemologists to describe a gemstone's dispersive nature or lack thereof. Dispersion is a material property. The amount of fire demonstrated by a given gemstone is a function of the gemstone's facet angles, the polish quality, the lighting environment, the material's refractive index, the saturation of color, and the orientation of the viewer relative to the gemstone.

In imaging

In photographic and microscopic lenses, dispersion causes chromatic aberration, which causes the different colors in the image not to overlap properly. Various techniques have been developed to counteract this, such as the use of achromats, multielement lenses with glasses of different dispersion. They are constructed in such a way that the chromatic aberrations of the different parts cancel out.

Pulsar emissions

Pulsars are spinning neutron stars that emit pulses at very regular intervals ranging from milliseconds to seconds. Astronomers believe that the pulses are emitted simultaneously over a wide range of frequencies. However, as observed on Earth, the components of each pulse emitted at higher radio frequencies arrive before those emitted at lower frequencies. This dispersion occurs because of the ionized component of the interstellar medium, mainly the free electrons, which make the group velocity frequency dependent. The extra delay added at a frequency is
:$t = k_\mathrm \cdot \left(\frac\right)$

where the dispersion constant ''k''_DM is given by
:$k_\mathrm = \frac \simeq 4.149\, \mathrm^2\,\mathrm^\,\mathrm^3\,\mathrm ,$

and the dispersion measure (DM) is the column density of free electrons (total electron content) — i.e. the number density of electrons ''n''_e (electrons/cm³) integrated along the path traveled by the photon from the pulsar to the Earth — and is given by
:$\mathrm = \int_0^d$

with units of parsecs per cubic centimetre (1 pc/cm³ = 30.857 × 10²¹ m⁻²).Lorimer, D.R., and Kramer, M., ''Handbook of Pulsar Astronomy'', vol. 4 of Cambridge Observing Handbooks for Research Astronomers, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A, 2005), 1st edition.

Typically for astronomical observations, this delay cannot be measured directly, since the emission time is unknown. What ''can'' be measured is the difference in arrival times at two different frequencies. The delay Δ''t'' between a high frequency _hi and a low frequency _lo component of a pulse will be
:$\Delta t = k_\mathrm \cdot \mathrm \cdot \left( \frac - \frac \right)$

Rewriting the above equation in terms of Δ''t'' allows one to determine the DM by measuring pulse arrival times at multiple frequencies. This in turn can be used to study the interstellar medium, as well as allow for observations of pulsars at different frequencies to be combined.

See also

* Abbe number
* Calculation of glass properties incl. dispersion
* Cauchy's equation
* Dispersion relation
* Fast radio burst (astronomy)
* Fluctuation theorem
* Green–Kubo relations
* Group delay
* Intramodal dispersion
* Kramers–Kronig relations
* Linear response function
* Multiple-prism dispersion theory
* Sellmeier equation
* Ultrashort pulse
* Virtually imaged phased array

References

External links

Dispersive Wiki
– discussing the mathematical aspects of dispersion.


– Encyclopedia of Laser Physics and Technology

Animations demonstrating optical dispersion
by QED

Interactive webdemo for chromatic dispersion
Institute of Telecommunications, University of Stuttgart

{{Authority control

Glass physics
Optics